Skip to main content

Correlation (or Dependence)

WORK IN PROGRESS

Correlation is a statistical measure that describes the interdependence of two or more variables. It is a measure of how close two variables are to having a linear relationship with each other. The closer the correlation value is to -1 or 1, the stronger the relationship between the variables. The closer the correlation value is to 0, the weaker the relationship between the variables.

Warning

Correlation not imply causation.

Take a look in this graph:

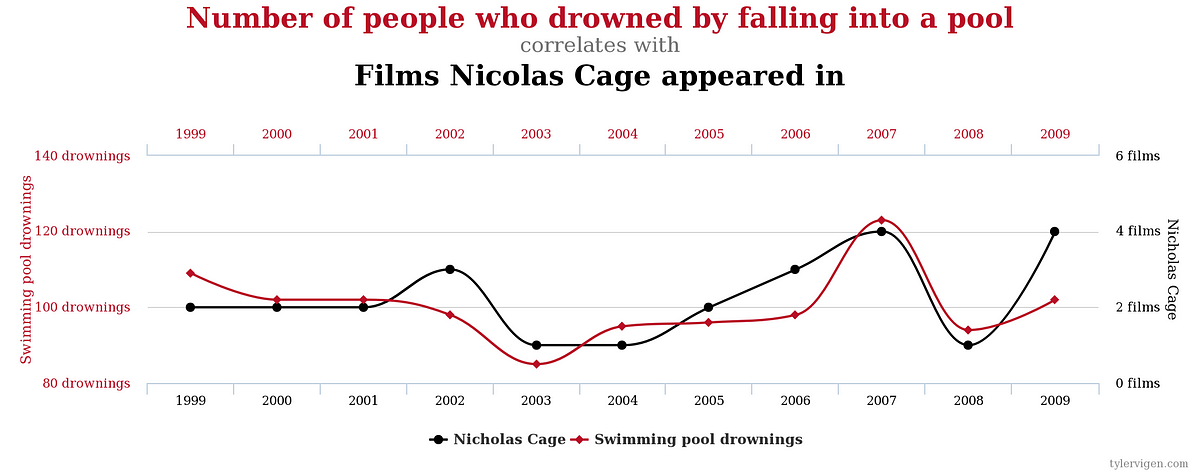
Alt text

The graph shows a strong correlation but it's obvious that it is a coincidence. The correlation is not a proof of causation.

Covariance

Before look at how to calculate the correlation, we need to understand about covariance.

Covariance is a measure of the joint variability of two random variables. It is a measure of how changes in one variable are associated with changes in a second variable. It is similar to variance, but where variance tells you how a single variable varies, covariance tells you how two variables vary together.

Pearson Correlation Coefficient

The Pearson correlation is commonly used in linear correlations. It is a measure of the linear correlation between two variables X and Y. It has a value between +1 and −1, where 1 is total positive linear correlation, 0 is no linear correlation, and −1 is total negative linear correlation.

pX,Y=CORR(X,Y)=COV(X,Y)σXσY=E[(X−μX)(Y−μY)]σXσY pX,Y = CORR(X, Y) = \frac{COV(X, Y)}{\sigma_X \sigma_Y} = \frac{E[(X - \mu_X)(Y - \mu_Y)]}{\sigma_X \sigma_Y}

Spearman Correlation Coefficient

The Spearman correlation is commonly used in non-linear correlations. It is a measure of the monotonicity of the relationship between two variables X and Y. It has a value between +1 and −1, where 1 is total positive monotonicity, 0 is no monotonicity, and −1 is total negative monotonicity.

ρ=COV(rank(X),rank(Y))σrank(X)σrank(Y)=E[(rank(X)−μrank(X))(rank(Y)−μrank(Y))]σrank(X)σrank(Y) \rho = \frac{COV(rank(X), rank(Y))}{\sigma_{rank(X)} \sigma_{rank(Y)}} = \frac{E[(rank(X) - \mu_{rank(X)})(rank(Y) - \mu_{rank(Y)})]}{\sigma_{rank(X)} \sigma_{rank(Y)}}

Kendall Correlation Coefficient

The Kendall correlation is commonly used in non-linear correlations. It is a measure of the ordinal association between two measured quantities. It has a value between +1 and −1, where 1 is total positive association, 0 is no association, and −1 is total negative association.

This is the most robust correlation coefficient. But is also the most computationally expensive.

P-value

P-value is the probability of obtaining test results at least as extreme as the results actually observed during the test, assuming that the null hypothesis is correct. The smaller the p-value, the stronger the evidence against the null hypothesis.

  • p < 0.001: strong evidence that the null hypothesis is false
  • p < 0.05: moderate evidence that the null hypothesis is false
  • p < 0.1: weak evidence that the null hypothesis is false
  • p > 0.1: no evidence that the null hypothesis is false

References

Joint probability distribution Correlation Correlation does not imply causation